
Математические модели в естественнонаучном образовании. Том II
Затем покажите, что вторая из этих формул может быть заменена на

б. Покажите, что на шаге 3 расстояния от



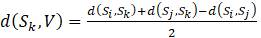
Таблица 5.11. Расстояния между таксонами для задачи 5.3.2

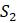



.83 .28 .41
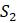
.72 .97

.48
5.3.2. Рассмотрим данные о расстояниях, приведенные в таблице 5.11. Используйте алгоритм присоединения соседей для построения дерева следующим образом:
а. Вычислите
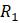





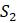





б. Если правильно справились с частью (а), то должно получиться несколько пар, имеющих одинаковое наименьшее значение




Для новой вершины





в. Вычислите


Поместите свои ответы в новую версию таблицы расстояний 5.12.
г. Поскольку осталось только 3 таксона, используйте 3-точечные формулы, чтобы поместить

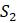

д. Нарисуйте последнее дерево, присоединив



Таблица 5.12. Групповые расстояния для задачи 5.3.2

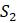


? ?
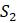
.72
Таблица 5.13. Расстояния таксонов для задачи 5.3.3

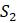



.3 .4 .5
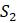
.5 .4

.7
5.3.3. Рассмотрим данные о расстояниях в таблице 5.13, которые точно соответствуют дереву с рисунка 5.15, при
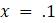

а. Используйте UPGMA для восстановления дерева на основе этих данных. Применим ли этот метод?
б. Используйте метод присоединения соседей, чтобы восстановить дерево из этих данных. Применим ли этот метод?
5.3.4. Выполните алгоритм присоединения соседей на данных о расстояниях, используемых в примерах из раздела 5.2. Чтобы использовать MATLAB для этого в первом примере, введите массив расстояний D=[0 .45 .27 .53; 0 0 .40 .50; 0 0 0 .62; 0 0 0 0] и названия таксонов Taxa={'S1','S2','S3','S4'}, затем запрограммируйте функцию nj, реализующую построение дерева методом присоединения соседей, чтобы можно было её использовать nj(D,Taxa{:}).
а. Построит ли метод присоединения соседей на примере с 4 таксонами то же самое дерево, что и метод UPGMA?
б. Производит ли метод присоединения соседей на примере с 5 таксонами то же самое дерево, что и FM-алгоритм?
5.3.5. Используйте расстояние Джукса-Кантора и программу построения деревьев методом присоединения соседей из предыдущей задачи для смоделированных данных последовательности ранее сохранённых в seqdata.mat. Сравните полученные результаты с результатами, полученными другими методами в задачах 5.2.9-5.2.12 предыдущего раздела. Как повлияли на результаты молекулярные часы, работающие в симуляции?
а. Данные a1, a2, a3 и a4 смоделируйте в предположении с молекулярными часами
б. Данные b1, b2, b3, b4 и b5 смоделируйте без молекулярных часов.
5.3.6. Сгенерируйте с использованием 2-параметической модели Кимуры последовательности c1, c2, c3, c4, c5 и сохраните их в seqdata.mat.
а. Даже не зная заранее, какая именно модель была использована, как сравнение некоторых из этих последовательностей поможет определить, что именно 2-параметрическое расстояние Кимуры было бы хорошим выбором для моделирования этих последовательностей?
б. Постройте дерево методом присоединения соседей, используя значение расстояния вычисляемого 2-параметрическим методом Кимуры.
в. Соответствует ли полученное дерево гипотезе молекулярных часов хотя бы приближенно? Обоснуйте свою точку зрения.
5.3.7. Сохраните последовательности d1, d2, d3, d4, d5 и d6 в файл seqdata.mat.
а. Выберите формулу расстояния для использования на этих последовательностях и объясните, почему сделанный выбор оптимален.
б. Постройте дерево методом присоединения соседей из имеющихся данных.
в. Один из этих 6 таксонов является внешней группой, которая была включена для того, чтобы получить корневое дерево на оставшихся 5. Какая именно из них является внешней группой? Нарисуйте корневое метрическое дерево, относящее к оставшимся таксонам.
5.4. Построение дерева методом максимальной экономии
Одним из критических недостатков дистанционных методов построения дерева заключается в том, что, поскольку они начинаются со сведения полных данных о последовательности ДНК к набору попарных расстояний между таксонами, то они могут не использовать всю информацию об исходных последовательностях.
Метод максимальной экономии предполагает несколько иной подход к построению дерева, использующий целые последовательности. Среди всех возможных деревьев, которые могут связывать таксоны, он ищет то, которое потребовало бы наименьшего количества возможных мутаций. Чтобы оценить количество мутаций никогда не вычисляются расстояния, а вместо этого рассматривается, как мутации происходят в имеющихся последовательностях на каждом отдельном участке.
Общий план таков: для данного дерева каким-то образом подсчитывается наименьшее количество мутаций, которое потребовалось бы, если бы последовательности возникли от общего предка в соответствии с этим деревом. Это число называется скупой оценкой дерева. Далее одно за другим рассматриваются все деревья, которые могут связать интересующие таксоны, и вычисляется оценку экономии для каждого из них. Затем выбирается дерево, которое имеет наименьшую оценку экономии. Это дерево, самое экономное, является тем, которое метод считает оптимальным для имеющихся данных о мутирующей последовательности.
В качестве первого шага реализации намеченного плана понадобится найти способ вычисления оценки экономии для определенного дерева и последовательностей. Предположим, что смотрим на один участок в ДНК для каждого из таксонов и видим, например,

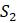


Если представить, что они были связаны деревом, показанным на рисунке 5.18, то можно пройти обратно вверх по дереву, чтобы определить, какое основание могло быть на этом на каждой внутренней вершине, предполагая наименьшее количество возможных мутаций.

Рисунок 5.18. Вычисление оценки экономии для дерева на одном сайте.
Например, выше




Продолжая продвигаться вверх по дереву, помещаем основание или набор возможных оснований на каждой вершине. Если под вершиной находятся два разных основания (или множества оснований, которые не пересекаются), нужно будет увеличить количество мутаций на 1 и объединить два основания (или взять объединение множеств) в один больший набор возможных оснований на более высокой вершине. Если два низших основания согласуются (или множества имеют общие элементы), то обозначаем высшую вершину этим основанием (или пересечением двух множеств). В этом случае не нужно подсчитывать дополнительную мутацию. Когда все вершины дерева помечены, конечное значение количества мутаций дает минимальное количество мутаций, необходимое для того, чтобы это дерево правильно описало эволюцию таксонов. Таким образом, дерево на рисунке 5.18 будет иметь минимальное количество мутаций, или показатель экономии, равный 3.
На самом деле есть несколько важных фактов, которые здесь использовались без доказательства. Во-первых, не совсем очевидно, что изложенный метод дает минимально возможное количество мутаций, необходимые для построения дерева. Хотя это должно казаться очевидным и на самом деле верно, что нет возможности назначать основания внутренним вершинам таким способом, который потребует меньшего количества мутаций, но не будем углубляться в строгое доказательство этого средствами комбинаторной теории графов. Как увидите в упражнениях, могут существовать такие разметки оснований на внутренних вершинах, которые не согласуются с разметками, производимыми данным методом, но при этом достигается то же самое минимальное количество мутаций. Это означает, что невозможно интерпретировать изложенный метод вычисления показателя экономичности как однозначную «реконструкцию» последовательности предков таксонов.
Во-вторых, показатель экономии дерева не зависит от расположения корня. Если используется одно и то же дерево, но корень перемещается, то данный метод подсчета может привести к тому, что поставим разные основания или наборы оснований в каждой из вершин. Тем не менее, можно доказать, что будет получен тот же коэффициент экономии. Таким образом, в то время как процедура подсчета требует временной вставки корня, в действительности можно говорить о пригодности некорневого дерева. Однако всегда можно добавить внешнюю вершину, как обсуждалось в предыдущих разделах, если требуется такое расположение корня.
Наконец, поскольку метод не позволяет однозначно восстановить последовательности на внутренних вершинах, то нет возможности узнать, вдоль каких ребер происходили мутации. Это означает, что не получится определить точную длину ребра, используя количество мутаций, происходящих при переходе вдоль него. Таким образом, метод максимальной экономии – это метод, который фокусируется только вокруг использования некорневых топологических деревьев для отыскания связей таксонов.
Теперь, когда получили оценку экономии дерева на рисунке 5.18, давайте рассмотрим другое дерево, на рисунке 5.19, которое может относиться к тем же 1-базовым последовательностям. Имейте в виду, дерево рисуется с корнем только для удобства. Применяя предыдущий метод для получения маркировки на внутренних вершинах, приходим к тому, что это дерево имеет оценку экономии 2; то есть необходимы только две мутации. Таким образом, дерево на рисунке 5.19 является более экономным, чем на рисунке 5.18.
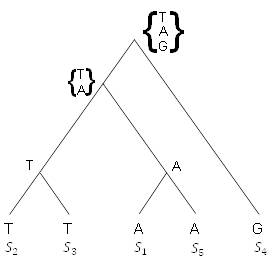
Рисунок 5.19. Более экономное дерево.
Чтобы найти наиболее экономное дерево для этих таксонов, нужно было бы рассмотреть все 15 возможных топологий некорневых деревьев с 5 таксонами и вычислить минимальное количество мутаций для каждой. Вместо того, чтобы перебирать 13 оставшихся деревьев, давайте попробуем подумать о том, какие деревья, вероятно, будут иметь низкие показатели экономии. Если оценка низкая, то

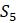
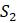


Вопросы для самопроверки:
– Для 5 таксонов нарисуйте несколько некорневых деревьев, которые топологически отличаются от изображенных на рисунке 5.19, но также имеют оценку экономии 2.
– Объясните, почему ни одно дерево, относящееся к этим 5 таксонам, не может иметь оценку экономии 1. Подсказка: если бы для дерева требовалась только одна мутация, то как выглядели бы основания на листьях?
Существует несколько деревьев (на самом деле, пять деревьев имеют оценку экономии 2), которые можно считать наиболее экономными. Когда это происходит, использование метода экономии требует отчета обо всех найденных деревьях, которые достигают минимального балла, потому что все они одинаково хороши согласно сформулированным критериям их выбора.
При работе с реальными данными последовательности, конечно, нужно подсчитать количество мутаций, необходимых для дерева, среди всех сайтов в последовательностях. Это можно сделать так же, как и раньше, просто обрабатывая каждый сайт параллельно. Пример приведём на рисунке 5.20.

Рисунок 5.20. Вычисление оценки экономии для дерева на трех участках.
Переходя вверх по дереву, начиная с 2 последовательностей таксонов, ATC и ACC в крайнем левом углу, видим, что там не нужны мутации ни в первом, ни в третьем узлах, но понадобятся мутации во втором. Таким образом, количество мутаций теперь равно 1, а вершина предка помечена, как показано на рисунке. На вершине, где соединяется ребро из третьего таксона, обнаруживаем, что первый участок нуждается в мутации, второй нет, а третий снова нуждается. Это увеличивает количество мутаций на 2, чтобы суммарно дать 3. Наконец, в корне обнаруживаем, что нужна мутация только во втором месте, для окончательной оценки экономии 4.
Хотя это нетрудно сделать вручную с небольшим количеством сайтов, когда считается много сайтов, это становится очень трудоёмкой задачей. Хуже то, что если есть взять еще немного таксонов, то количество топологий деревьев, которые необходимо учитывать, огромно. Таким образом, метод экономии на практике выполняется только с помощью компьютера. На самом деле, при большом количестве таксонов количество возможных деревьев настолько велико, что часто компьютерные программы проверяют не все, а только определенные конфигурации, чтобы выбрать наиболее экономное сочетание. Хорошее программное обеспечение, управляемое профессиональными пользователями, часто поможет найти то, что, вероятно, будет самыми экономными деревьями, но в этом нет никакой гарантии. Это вызывает некоторое смущение у исследователей, публикующих деревья, найденные машинным перебором. Так как, не имея малейшего представления, насколько хороши найденные варианты, им приходится использовать то, что есть, пока фактически случайным образом не будет найдено ещё более оптимальной конфигурации.
Можно исключить некоторые варианты из перебора при использовании метода экономии, если заметим, что не все сайты будут влиять на количество мутаций, необходимых для дерева. Очевидным случаем является то, что если все последовательности имеют одно и то же основание в определенном сайте, то всем деревьям потребуется 0 мутаций для этого сайта. Таким образом, можем исключить этот сайт из последовательностей перед применением алгоритма. Менее очевиден случай, когда в сайте все последовательности имеют одно и то же основание (например, А), за исключением не более чем одной последовательности, каждая из которых имеет другие основания (С, Т и G). В этом случае, независимо от топологии дерева, если поставим A в каждой внутренней вершине, то получим минимально возможное количество мутаций. Это означает, что такой сайт не повлияет на то, какое дерево выберем как самое экономное. Данная возможность приводит к возникновению следующего понятия.
Определение. Информативный сайт – это сайт, на котором по крайней мере два разных основания встречаются как минимум по два раза каждое среди рассматриваемых последовательностей.
Прежде чем применять алгоритм экономии, можем исключить все неинформативные сайты из последовательностей, потому что они не повлияют на выбор самого экономного дерева. Обратите внимание, что в предыдущих примерах использовались только информативные сайты.
Метод максимальной экономии не использует ни модель молекулярной эволюции Джукса-Кантора, ни какую-либо другую явную модель мутации ДНК. Вместо этого метод подразумевает неявное предположение о том, что мутации случаются редко, а лучшее объяснение истории эволюции – это то, которое требует наименьшего количества мутаций. Между исследователями, выступающими за основанные на перечисленных моделях методы реконструкции эволюционных деревьев, и теми, кто выступает за метод экономии, велись ожесточенные, а иногда и жесткие споры. Вместо того, чтобы присоединяться к философскому спору, просто отметим, что, когда есть несколько мутаций, скрывающих предыдущие мутации, то и методы дистанцирования, и методы экономии, по-видимому, на практике работают достаточно хорошо. Предположения каждого из методов могут быть подвергнуты обоснованной критике, и многое еще предстоит сделать, чтобы найти лучшие решения.
Задачи для самостоятельного решения:
5.4.1. а. Вычислите минимальное количество базовых изменений, необходимых для деревьев на рисунке 5.21.

Рисунок 5.21. Деревья для задачи 5.4.1.
б. Дайте по крайней мере три дерева, которые связывают наиболее экономные последовательности с одним основанием, используемые в части (a). Помните: можно перечислять таксоны в другом порядке.
в. Среди деревьев, прослеживающих эволюцию только на одном участке, как в частях (а) и (б), почему всегда можно найти дерево, требующее не более трех замен, независимо от того, сколько таксонов присутствует?
5.4.2. а. Найдите оценку экономии деревьев, изображенных на рисунке 5.22, где показаны только информативные сайты в последовательностях ДНК.
б. Нарисуйте третье возможное (некорневое) топологическое дерево, относящееся к этим последовательностям, и найдите для него оценку экономии. Какое из трех деревьев является наиболее скупым?

Рисунок 5.22. Деревья для задачи 5.4.2.
5.4.3. Рассмотрим следующие последовательности из четырех таксонов.

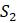


а. Какие сайты являются информативными?
б. Используйте информативные сайты, чтобы определить наиболее скупое некорневое дерево, относящееся к этим последовательностям.
в. Если известно, что


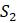

5.4.4. Хотя неинформативные сайты не влияют на то, какое дерево считается наиболее экономным, они влияют на показатель экономии. Объясните, почему, если













