Радиус наблюдаемой Вселенной и горизонт Вселенной

Мы рассматривали движение авто на вытягивающейся дорожке. Однако все приведённые рассуждения полностью соответствуют и движению фотона от некоторой сверхновой к Земле в расширяющемся пространстве Вселенной. Поэтому в итоговых уравнениях мы можем просто заменить скорость авто скоростью света:

Уравнение (10.3) показывает действительную величину удалённости фотонов от сверхновой, равенство (10.4) отражает равенство этой удалённости и конечной удалённости Земли от сверхновой. Это условие мы заложили в постановке задачи. Но из них следует и провозглашённый в задаче вывод. Всё движение, и авто и фотонов, происходило в течение времени T, что соответствует, в свою очередь, длине пройденного пути с точки зрения движущегося объекта – авто или фотонов. Действительно, на спидометре авто за это время при заданной скорости будет показан вполне определённый пройденный им путь:

Соответственно, и по условному "спидометру" фотонов или с точки зрения некоторого не менее условного внешнего наблюдателя в их системе отсчёта, фотоны пройдут путь:

Это и есть наблюдаемая удалённость сверхновой. Из этого уравнения следуют два вывода. С увеличением времени движения отношение наблюдаемой удалённости сверхновой к её действительной удалённости на момент измерения стремится к нулю:

Наблюдаемая удалённость сверхновой численно равна времени от её взрыва до момента её наблюдения (при с = 1).

Анализ погрешностей алгоритма

Приведённый алгоритм является пошаговым, точность вычислений которого, очевидно, зависит от дискретности этих шагов. Чем меньше интервал времени шага, тем, видимо, точнее результат вычислений. Кроме того, рассмотренное вычисление пути возможно в двух вариантах первого шага, что, возможно, также влияет на итог вычисления, и, фактически, на его точность. Рассмотрим эти два варианта для оценки их точности.

Пусть, как и выше, скорость авто равна v

, а общее время в пути ограничим временем T = 2 = 2t. Также примем удлинение "резиновой" трассы по экспоненте – увеличение в e

раз за каждую единицу времени.

Вариант 1. От начальной дистанции r

за время t = 1 сначала прошёл свой путь авто. И только после этого за следующий интервал времени t = 1 этот путь экспоненциально удлинился:

Вариант 2. За первый интервал времени t = 1 сначала экспоненциально удлинилась исходная дистанция, и только затем свой путь прошёл авто за оставшееся время t = 1:

В первом варианте авто прошёл большее расстояние:

Теперь рассмотрим следующие два интервала времени, то есть, увеличим общее время в пути до T = 4. Начальным, исходным путём на этих дополнительных интервалах являются, соответственно, R

и R

.

Преобразуем, раскрывая скобки и сокращая:

Здесь уже просматривается закономерность. Проверим ещё один этап движения, третий с общим временем, увеличенным до T = 6. В роли r

теперь выступают R

и R

.

Вновь вычисляем разницу:

Теперь закономерность видна явно. Очевидно, что для общего времени движения T = 2nt, то есть, через n-пар интервалов времени разница будет:

При уменьшении длительности интервалов, то есть, при увеличении их числа, разница стремится к величине:

При фиксированном значении времени T пределом является ноль, то есть, варианты эквивалентны:

Заметим, что это можно обнаружить изначально. В случае r

 = 0, то есть, если движение начинается из начала координат, второй вариант сразу же переходит в первый:

Следует признать, что алгоритм вычислений несколько условный, приближённый, поскольку подразумевает всё-таки поочерёдное удлинение пройденного интервала и прироста интервала за счёт движения авто. Вместе с тем, оба уравнения при большом значении числа интервалов n и при некотором фиксированном значении общего времени T движения дают одинаковый результат. Последовательность приростов дистанции не влияет на результат, что следует рассматривать как корректность алгоритма вычислений и его приемлемую точность.

Радиус наблюдаемой Вселенной

В литературе зачастую приводятся довольно спорные определения радиуса наблюдаемой Вселенной. Предлагаем такой вариант: радиусом наблюдаемой Вселенной следует считать расстояние на момент начала расширения пространства, расстояние до самой дальней галактики, которую мы в принципе можем наблюдать (или наблюдаем) сегодня. Ключевые условия – начало и сегодня. Это означает, что в каждую эпоху этот радиус различный, а сверхдальние галактики, которые мы сегодня пока наблюдать не можем, в более позднее время всё-таки станут для нас видимыми. Принципиальное отличие нашего определения от традиционного (горизонт частиц), как видим, состоит в том, что это исходная удалённость объекта, а не та, на которой он находится в наши дни. Здесь важным является то, что называть наблюдаемой нынешнюю удалённость этого самого удалённого объекта неверно: как он выглядит сегодня, нам не только неизвестно, но и в общем случае не может быть определено никогда.

Для того чтобы вычислить величину радиуса наблюдаемой Вселенной, сформулируем задачу в следующем виде: какой должна быть удалённость сверхновой, чтобы за время существования Вселенной свет от неё достиг Земли. Найти исходную удалённость самой дальней сверхновой, которая может быть видна в наши дни, мы сможем, используя выведенное уравнение (10.4). Для этого сначала вычисляем путь, пройденный светом за время существования Вселенной, затем по этому времени определяем и исходную удалённость сверхновой.

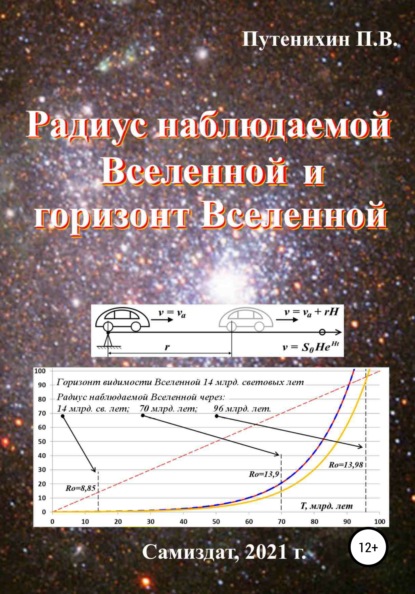
На следующей диаграмме, в системе отсчёта сверхновой показаны графики движения, удаления Земли от галактики, скорость её удаления и графики реального движения фотонов (красная линия) и видимого с Земли света (красная штриховая линия) – рис.10.2.

График движения света от начала расширения пространства, света, испущенный сверхновой показан на рисунке красной линией R_exp. Экспоненциальная форма графика движения фотонов вызвана тем, что к скорости фотона постоянно добавляется скорость "носителя света" – расширяющегося пространства.

Как видим, на момент получения света на Земле галактика будет находиться от неё на удалении в 24 млрд. световых лет. Начальную удалённость галактики от Земли, при которой в процессе расширения пространства она удалится на это же расстояние, определим обратным вычислением по уравнению движения, показанного синим графиком R. Находим, что это 8,85 млрд. световых лет. Галактика, находившаяся в начале расширения пространства именно на этом удалении от Земли, удалится от неё на 24 млрд. световых лет, на такое же расстояние, на какое фотоны вспышки удалились от неё.

Рис.10.2

Понятно, что это самая дальняя галактика на момент начала расширения пространства, свет от которой смог достичь Земли за 14 млрд. лет (время отмечено вертикальной штриховой линией T14). Это так, поскольку мы рассмотрели именно самое большое расстояние, какое смог пройти свет за это время. При этом видна галактика будет так, будто она находится не на расстоянии 8,85 или 24, а на расстоянии 14 млрд. световых лет (кратко – Гсл – Гига-световых лет). Об этом свидетельствует тонкая красная штриховая линия Rco – график кажущегося движения света, то есть, без учёта космологического расширения пространства, согласно (10.3). Это означает, что время движения света определяется не по теоретической (8,85 Гсл) или конечной (24 Гсл), а по наблюдаемой удалённости его источника, определяемой в свою очередь по его яркости.

Графики на диаграмме создают впечатление, будто фотоны прошли более длинный путь R_exp, поскольку график его движения, красная линия R_exp завершена в точке с удалённостью в 24 млрд. световых лет, а штриховая Rco – учитываемая, наблюдаемая удалённость источника фотонов – в точке 14 млрд. световых лет. Однако выше мы вывели уравнение движения фотонов вспышки и пришли к выводу, что реально фотоны прошли всё-таки меньший путь (здесь – 14), чем конечная удалённость (24) сверхновой от Земли. На самом деле в этом нет противоречия, поскольку меньший путь, который мы вычислили, и есть путь Rco, показанный штриховой линией. Красная линия R_exp является реальным графиком движения фотонов со сверхсветовой скоростью, указывающим их удалённость во времени от точки взрыва сверхновой. В наши дни график завершается в точке наблюдения на Земле, в 24 млрд. световых лет. Однако за это же время в 14 млрд. лет по собственным часам фотонов, они прошли путь, изображённый штриховой линией Rco – это фактически пройденный фотонами путь – 14 млрд. световых лет. Иначе говоря, для фотонов вся трасса как бы делится на две части: одна впереди, перед ними, а другая – позади них. Первую трассу, впереди фотоны проходили уже после того, как она испытала экспоненциальное удлинение. Вторая часть трассы, позади них расширялась уже после того, как фотоны ушли вперёд. Поэтому общая длина трассы R_exp оказывается больше пути фотонов Rco на величину удлинения за время движения после того, как фотоны сместились вперёд. Буквально это означает, что фотоны удалились на 24 млрд. световых лет, пройдя при этом путь только в 14 млрд. световых лет. Можно интерпретировать это и так, будто сферический фронт света не просто расширяется в пространстве, а ещё и переносится вперёд, перемещается "в замороженном виде" к наблюдателю.

Рис.10.3

Пересечение синей линии R, графика удаления Земли от сверхновой, с красной R_exp, графика удаления фотонов от сверхновой, означает, что Земля и фотоны находятся на одном и том же удалении от сверхновой, в одной и той же точке пространства, то есть, фотоны достигли наблюдателей на Земле.

Жёлтая линия v – это скорость Земли относительно сверхновой: видно, что эта скорость удаления в наши дни уже превысила 1,7 скоростей света (график показан в масштабе с 10-кратным увеличением).

Если сверхновая находится в начальный момент времени t = 0 на большем удалении, чем 8,85 млрд. световых лет, но меньшем, чем горизонт видимости Вселенной, то с Земли она будет видна только в будущем, в более позднее время. Например, свет от галактики, находившейся на удалении около 9 млрд. световых лет, Земли пока не достиг. На рисунке видно, что линии удалённости галактики (синяя) и светового потока от взрыва сверхновой (красная) явно пересекутся, но не в наши дни – 14 млрд. лет, а позднее.

Рис.10.4

Отметим, что расстояние R_exp между фотонами вспышки и наблюдателем на Земле R постоянно уменьшается. Если в начальный момент расстояние между звездой, фотонами её вспышки и Землёй было 9 млрд. световых лет, то через 5 млрд. лет оно уменьшилось до ~ 6,8 млрд. световых лет, а через 10 млрд. лет – до ~ 4 млрд. световых лет.

Рис.10.5

Если же в момент вспышки сверхновая находилась на меньшем удалении, чем 8,85 млрд. световых лет, то есть, ближе радиуса наблюдаемой Вселенной, то свет от неё уже был получен в прошлом. Например, на рисунке 10.5 показана звезда, которая в начальный момент находилась от Земли на удалении в 1 млрд. световых лет. Наблюдателем на Земле получен свет от вспышки этой сверхновой, произошедшей 4 млрд. лет назад. Также в прошлом был получен и свет от вспышки, примерно 2 млрд. лет назад.

Сегодня эта галактика находится от Земли на расстоянии в ~2,7 млрд. световых лет, а свет от неё наблюдается в виде старых остатков от взрыва. Виден этот свет от остатков сверхновой в наши дни на удалении 2,5 млрд. световых лет, хотя, как указано, остатки сверхновой реально находятся на удалении в ~2,7 млрд. световых лет.

Приведённые выкладки верны только для галактик, которые находятся ближе горизонта видимости Вселенной, поскольку более удалённые галактики нам не видны.

Горизонт видимости Вселенной

Здесь нам следует внести уточнение понятию горизонта видимости Вселенной и его соотношению с радиусомнаблюдаемой Вселенной. Горизонтом видимости Вселенной (в литературе – горизонт событий) следует считать исходное, в начальный момент расширения расстояние до самой дальней галактики, которую мы можем наблюдать в принципе, пусть даже и через бесконечно большое время. Физически горизонтом видимости Вселенной является радиус сферы Хаббла, который определяется параметром Хаббла и изменяется при его изменении: