По всем вопросам обращайтесь на: info@litportal.ru
(©) 2003-2024.
✖
Силы тяготения внутри обруча, сферы и между двух точек
Автор
Год написания книги
2021
Настройки чтения
Размер шрифта
Высота строк
Поля
Силы тяготения внутри обруча, сферы и между двух точек
Петр Путенихин
Рассмотрены силы, действующие на пробное тело внутри обруча, полой сферы и между двумя массивными точками. По мере удаления от центра системы сила притяжения растёт от нуля до некоторого максимума. Утверждение об отсутствии сил тяготения внутри полой сферы является ошибочным. The forces acting on a test body inside a hoop, a hollow sphere, and between two massive points are considered. With distance from the center of the system, the force of attraction grows from zero to a certain maximum. The statement about the absence of gravitational forces inside the hollow sphere is erroneous.
Петр Путенихин
Силы тяготения внутри обруча, сферы и между двух точек
1. Притяжение тела внутри обруча
Считается, что тело внутри полой сферы не испытывает сил притяжения с её стороны. Рассмотрим такую же ситуацию в плоской форме – силу притяжения тела внутри полого цилиндра. Более того, будем считать, что высота цилиндра равна нулю. Фактически это круг с круглым отверстием внутри.
Очевидно, что ширина этой круговой полосы также качественно не влияет на результаты вычислений, поэтому будем считать её также равной нулю, то есть, рассмотрим очень тонкий массивный обруч.
Для точного определения сил, действующих на тело внутри обруча, рассмотрим дифференциал массы обруча, массу каждого элементарного, бесконечно малого его участка, которая равна
Определим расстояние r между массой m и дифференциальным элементом
Рис.1.1.Определение силы притяжения тела внутри обруча.
С учетом m = 1, ? = 1 и вычисленного квадрата радиуса сила притяжения равна
Нас интересует сила, направленная вдоль оси X. Определяем её из соотношения подобных треугольников
Заменим Rx на долю от R
, то есть, Rx = kR
, где, очевидно, k = 0…1
Вычисляем значение силы для каждого значения R
или значения k. Очевидно, что ни одно из значений силы, кроме k = 0, не равно нулю. При этом значении интеграл упрощается до элементарного
Вероятно, значение силы тем больше, чем ближе R
к R
. При этом следует ожидать даже бесконечно больших значений при значении k = 1
В точке ? = 0 подынтегральная функция обращается в неопределённость, деление нуля – d? на ноль. Попробуем разрешить эту неопределённость. Поскольку мы производим численное интегрирование, то эта точка соответствует конечным, компьютерным значениям дифференциала и функции ? = d? =0, то есть, неопределённость 0/0
Попробуем разрешить неопределённость аналитически. Вблизи этой точки дифференциал d? и аргумент ? одинаково стремятся к нулю, поэтом обозначим их одной переменной. Найдём предел отношения подынтегральной функции
Известно, что предел отношения функций равен пределу отношения их производных
Повторим процедуру замены функций на их производные
Ранее мы извлекли функцию из-под корня, теперь возвращаем
Казалось бы, при нулевом расстоянии между фрагментом обруча и материальной точкой m сила притяжения должна быть равна бесконечность. Однако мы рассматриваем одновременно с уменьшением дистанции и уменьшение длины этого фрагмента, что и привело к конечному значению неопределённости. Другим объяснением может служить то, что расстояние между объектом m и элементом обруча при стремлении его к нулю фактически заменяется в пределе их слиянием. Теперь это не расстояние между ними, это их общий размер. Иначе говоря, два элемента слились своими центрами, а на тело, находящееся в центре массивного объекта, не действуют никакие силы.
Проверяем решение численным интегрированием (1.3).
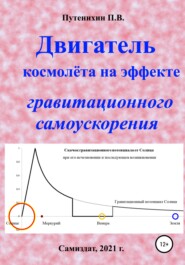
Рис.1.2. График изменения силы притяжения пробного тела внутри обруча в зависимости от его удалённости от центра. График приведён полностью
Диапазон изменения сил оказался слишком большим, поэтому график плохо просматривается. Все его значения почти на 95% длины радиусов выглядят нулевыми. Чтобы сжать график до размеров диаграммы, можно использовать логарифм величины. Понятно, что отрицательные значения в начале графика соответствуют его значениям, меньшим единицы.
Рис.1.3. Логарифмический график изменения силы притяжения внутри обруча пробного тела в зависимости от его удалённости от центра
Без логарифма, с частичным отсечением верхних значений график выглядит на всём интервале возрастающим
Рис.1.4. График изменения силы притяжения пробного тела внутри обруча в зависимости от его удалённости от центра. Максимальные значения частично отсечены.
Если ещё больше увеличить масштаб начального интервала, увеличить отсечение сверху, то будет видна практически параболическая или экспоненциальная зависимость
Рис.1.5. График изменения силы притяжения внутри обруча пробного тела в зависимости от его удалённости от центра. Максимальные значения отсечены.
Интеграл силы (1.3) мы формировали исходя из положительного направления силы в сторону центра обруча. Интегрирование и графики показали положительное значение силы. Из этого следует вывод: тело в пустом обруче притягивается к его центру так, будто там находится некий массивный объект.
Главной целью наших исследования сил притяжения в обруче является определение необходимости учёта этих сил при исследовании гравитационных сил в однородном диске, являющемся аналогом дисковой галактики. Наличие такой внутренней силы ведёт к формированию специфических кривых вращения, например, подобных наблюдаемой кривой вращения галактики Млечный Путь [4].
2. Притяжение тела внутри сферы
Вычислим силу притяжения тела массой m = 1, находящегося на удалении Rx от центра сферы радиусом R
. Каждый бесконечно малый, дифференциальный объём dv сферы массой dM притягивает тело m независимо от других её элементов, составляющих
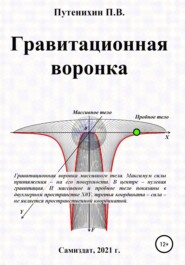
Рис.2.1. Определение дифференциала площади сферы для нахождения силы притяжения пробного тела внутри сферы
На рисунке видно, что две плоскости, одна из которых – плоскость X0Y, вырезают на сфере "апельсиновую дольку" с углом d?. На её поверхности, на "кожуре" ещё две плоскости с углом между ними d? вырезают участок площадью ds. Можно заметить, что все "апельсиновые дольки" равны друг другу и не зависят от собственного угла ?, поэтому мы приняли его равным d?. Поэтому нам достаточно рассмотреть только одну из них и затем умножить на число этих долек. Число долек определяется в свою очередь от их ширины:
Если взять их ширину бесконечно малой, то число этих долек станет равным бесконечности. Однако их суммарная площадь равна, как видим, полному углу
Напротив, другая сторона дифференциальной площади ds зависит от угла ? дважды – непосредственно, по образующей вдоль дольки и через зависимость ортогональной стороны, образованной углом d?, зависящей также и от угла ?.
Действительно, как видно на рисунке ширина дольки разная, в зависимости от угла ?. Самая широкая её часть находится в плоскости Z0Y, а вблизи плоскости Z0X ширина дольки сводится к нулю. Зависимость эта от угла ? описывается уравнением R
sin?d?. Таким образом, площадь дифференциального участка сферы описывается уравнением
С учетом принятого выше условия равенства всех дифференциальных "апельсиновых долек" это уравнение приобретает вид
Для удобства дальнейших рассуждений рассмотрим другой рисунок, менее перегруженный линиями. Этот рисунок мы использовали при вычислении сил, действующих на объект внутри обруча. В данном случае мы будем помнить, что площадь дифференциального участка описывается новым уравнением (2.1)
Рис.2.2. Определение расстояния между дифференциалом площади сферы и пробного тела внутри сферы
Дифференциал силы притяжения между пробным телом m и этим элементарным, дифференциальным участком сферы равна
Мы принимаем, что масса участка определяется неизменной поверхностной плотностью сферы. Поскольку мы приняли, что сфера имеет нулевую толщину, то вместо объёма сразу же указываем площадь. Дифференциал площади мы уже определили (2.1), теперь определим расстояние между объектом и этим участком сферы. Как видно на рисунке, оно описывается уравнением
Петр Путенихин
Рассмотрены силы, действующие на пробное тело внутри обруча, полой сферы и между двумя массивными точками. По мере удаления от центра системы сила притяжения растёт от нуля до некоторого максимума. Утверждение об отсутствии сил тяготения внутри полой сферы является ошибочным. The forces acting on a test body inside a hoop, a hollow sphere, and between two massive points are considered. With distance from the center of the system, the force of attraction grows from zero to a certain maximum. The statement about the absence of gravitational forces inside the hollow sphere is erroneous.
Петр Путенихин
Силы тяготения внутри обруча, сферы и между двух точек
1. Притяжение тела внутри обруча
Считается, что тело внутри полой сферы не испытывает сил притяжения с её стороны. Рассмотрим такую же ситуацию в плоской форме – силу притяжения тела внутри полого цилиндра. Более того, будем считать, что высота цилиндра равна нулю. Фактически это круг с круглым отверстием внутри.
Очевидно, что ширина этой круговой полосы также качественно не влияет на результаты вычислений, поэтому будем считать её также равной нулю, то есть, рассмотрим очень тонкий массивный обруч.
Для точного определения сил, действующих на тело внутри обруча, рассмотрим дифференциал массы обруча, массу каждого элементарного, бесконечно малого его участка, которая равна
Определим расстояние r между массой m и дифференциальным элементом
Рис.1.1.Определение силы притяжения тела внутри обруча.
С учетом m = 1, ? = 1 и вычисленного квадрата радиуса сила притяжения равна
Нас интересует сила, направленная вдоль оси X. Определяем её из соотношения подобных треугольников
Заменим Rx на долю от R
, то есть, Rx = kR
, где, очевидно, k = 0…1
Вычисляем значение силы для каждого значения R
или значения k. Очевидно, что ни одно из значений силы, кроме k = 0, не равно нулю. При этом значении интеграл упрощается до элементарного
Вероятно, значение силы тем больше, чем ближе R
к R
. При этом следует ожидать даже бесконечно больших значений при значении k = 1
В точке ? = 0 подынтегральная функция обращается в неопределённость, деление нуля – d? на ноль. Попробуем разрешить эту неопределённость. Поскольку мы производим численное интегрирование, то эта точка соответствует конечным, компьютерным значениям дифференциала и функции ? = d? =0, то есть, неопределённость 0/0
Попробуем разрешить неопределённость аналитически. Вблизи этой точки дифференциал d? и аргумент ? одинаково стремятся к нулю, поэтом обозначим их одной переменной. Найдём предел отношения подынтегральной функции
Известно, что предел отношения функций равен пределу отношения их производных
Повторим процедуру замены функций на их производные
Ранее мы извлекли функцию из-под корня, теперь возвращаем
Казалось бы, при нулевом расстоянии между фрагментом обруча и материальной точкой m сила притяжения должна быть равна бесконечность. Однако мы рассматриваем одновременно с уменьшением дистанции и уменьшение длины этого фрагмента, что и привело к конечному значению неопределённости. Другим объяснением может служить то, что расстояние между объектом m и элементом обруча при стремлении его к нулю фактически заменяется в пределе их слиянием. Теперь это не расстояние между ними, это их общий размер. Иначе говоря, два элемента слились своими центрами, а на тело, находящееся в центре массивного объекта, не действуют никакие силы.
Проверяем решение численным интегрированием (1.3).
Рис.1.2. График изменения силы притяжения пробного тела внутри обруча в зависимости от его удалённости от центра. График приведён полностью
Диапазон изменения сил оказался слишком большим, поэтому график плохо просматривается. Все его значения почти на 95% длины радиусов выглядят нулевыми. Чтобы сжать график до размеров диаграммы, можно использовать логарифм величины. Понятно, что отрицательные значения в начале графика соответствуют его значениям, меньшим единицы.
Рис.1.3. Логарифмический график изменения силы притяжения внутри обруча пробного тела в зависимости от его удалённости от центра
Без логарифма, с частичным отсечением верхних значений график выглядит на всём интервале возрастающим
Рис.1.4. График изменения силы притяжения пробного тела внутри обруча в зависимости от его удалённости от центра. Максимальные значения частично отсечены.
Если ещё больше увеличить масштаб начального интервала, увеличить отсечение сверху, то будет видна практически параболическая или экспоненциальная зависимость
Рис.1.5. График изменения силы притяжения внутри обруча пробного тела в зависимости от его удалённости от центра. Максимальные значения отсечены.
Интеграл силы (1.3) мы формировали исходя из положительного направления силы в сторону центра обруча. Интегрирование и графики показали положительное значение силы. Из этого следует вывод: тело в пустом обруче притягивается к его центру так, будто там находится некий массивный объект.
Главной целью наших исследования сил притяжения в обруче является определение необходимости учёта этих сил при исследовании гравитационных сил в однородном диске, являющемся аналогом дисковой галактики. Наличие такой внутренней силы ведёт к формированию специфических кривых вращения, например, подобных наблюдаемой кривой вращения галактики Млечный Путь [4].
2. Притяжение тела внутри сферы
Вычислим силу притяжения тела массой m = 1, находящегося на удалении Rx от центра сферы радиусом R
. Каждый бесконечно малый, дифференциальный объём dv сферы массой dM притягивает тело m независимо от других её элементов, составляющих
Рис.2.1. Определение дифференциала площади сферы для нахождения силы притяжения пробного тела внутри сферы
На рисунке видно, что две плоскости, одна из которых – плоскость X0Y, вырезают на сфере "апельсиновую дольку" с углом d?. На её поверхности, на "кожуре" ещё две плоскости с углом между ними d? вырезают участок площадью ds. Можно заметить, что все "апельсиновые дольки" равны друг другу и не зависят от собственного угла ?, поэтому мы приняли его равным d?. Поэтому нам достаточно рассмотреть только одну из них и затем умножить на число этих долек. Число долек определяется в свою очередь от их ширины:
Если взять их ширину бесконечно малой, то число этих долек станет равным бесконечности. Однако их суммарная площадь равна, как видим, полному углу
Напротив, другая сторона дифференциальной площади ds зависит от угла ? дважды – непосредственно, по образующей вдоль дольки и через зависимость ортогональной стороны, образованной углом d?, зависящей также и от угла ?.
Действительно, как видно на рисунке ширина дольки разная, в зависимости от угла ?. Самая широкая её часть находится в плоскости Z0Y, а вблизи плоскости Z0X ширина дольки сводится к нулю. Зависимость эта от угла ? описывается уравнением R
sin?d?. Таким образом, площадь дифференциального участка сферы описывается уравнением
С учетом принятого выше условия равенства всех дифференциальных "апельсиновых долек" это уравнение приобретает вид
Для удобства дальнейших рассуждений рассмотрим другой рисунок, менее перегруженный линиями. Этот рисунок мы использовали при вычислении сил, действующих на объект внутри обруча. В данном случае мы будем помнить, что площадь дифференциального участка описывается новым уравнением (2.1)
Рис.2.2. Определение расстояния между дифференциалом площади сферы и пробного тела внутри сферы
Дифференциал силы притяжения между пробным телом m и этим элементарным, дифференциальным участком сферы равна
Мы принимаем, что масса участка определяется неизменной поверхностной плотностью сферы. Поскольку мы приняли, что сфера имеет нулевую толщину, то вместо объёма сразу же указываем площадь. Дифференциал площади мы уже определили (2.1), теперь определим расстояние между объектом и этим участком сферы. Как видно на рисунке, оно описывается уравнением